2019年2月14日2019年11月24日

注意：この記事は間違っています！

「jay」さんという方からコメントを頂き誤りに気が付きました。

体重が減少しているのに力積を一定としているところに誤りがあります。

ジャンプ力は体重の２乗に反比例しません。

計算し直した所、体重に反比例すると考えられます。

修正するか記事を消そうか迷いましたが、間違っていることを敢えて乗っけておくことも大事だと思い消さないでおきます。

体重の２乗に反比例するならダイエットだ！と意気込んでしまったみなさんごめんなさい。

２乗には反比例しませんが、ダイエットでジャンプ力は間違いなくあがるのでそこだけは安心してください。

そのうち正しいと思われる体重とジャンプ力の関係を記事にします。

では以下の文章は力積を一定としたところが誤っていますので、読むのであれば気をつけて読んでください。

続・体重とジャンプ力の関係

修正した記事を作成しました。

以下、駄文

———————————————–

みなさん、ジャンプ力上げたいですか？

垂直跳び１００ｃｍって憧れませんか？

バスケやバレーボールをやっている選手であれば、ジャンプ力というのは圧倒的な武器になります。

ジャンプ力を上げる方法はたくさんありますが、中でもダイエットが一番簡単にジャンプ力を上げることができます。

痩せた時も筋力が変わらないと仮定した場合、体重90kgで高さ70cm跳べていた人は、20kg痩せて体重が70kgになった時、高さはなんと115cmも跳ぶことができます。

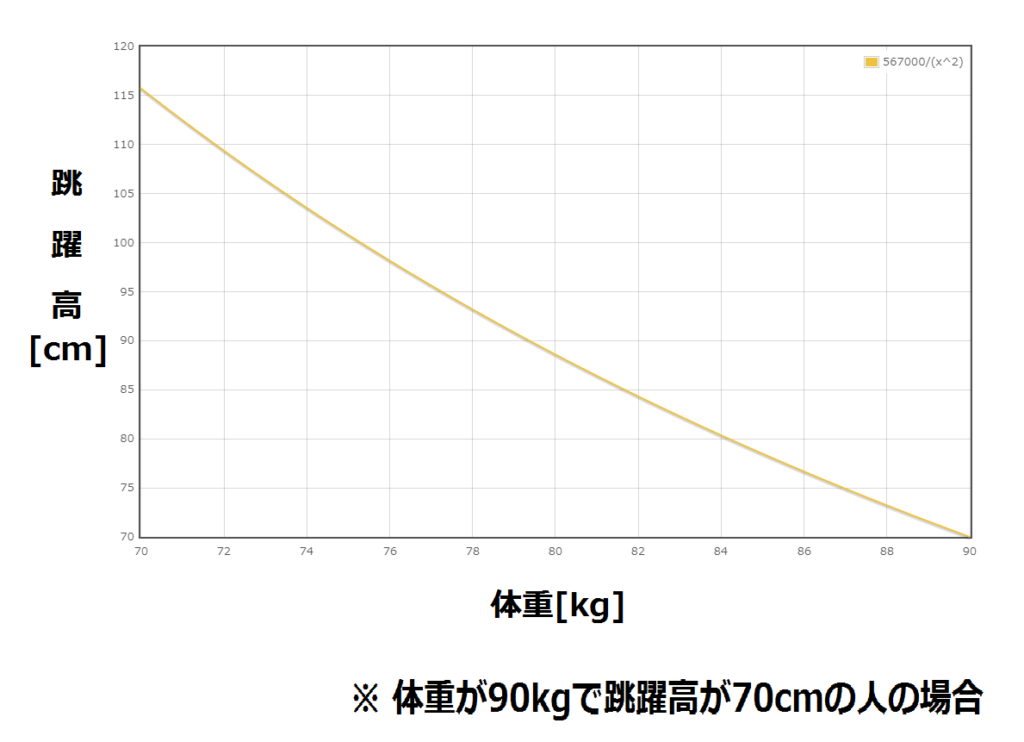
グラフはこんな感じになります。

後ほどで説明しますが、ジャンプ力は体重の２乗に反比例します。つまり軽ければ軽いほどジャンプ力は加速度的に伸びていきます。

身長が小さい人は、身長が高い人に比べて体重がかなり軽い傾向にあります。

アキレス腱の長さなどを考慮に入れなければ、高身長の人より低身長の人のほうがジャンプできる可能性があります。

実際には20kgも痩せてしまうと筋力もだいぶ落ちてしまうのでここまでの高さが跳べるかはわかりませんが、筋力を一定に保つことができれば115cmの高さに到達できるはずです。

（ダイエットではなく、手術による脂肪吸引によって体の脂肪を除去すれば筋力を落とさずに体重を減らすことができますが・・・。）

ここまでの話は高校物理の力学を知っていれば、簡単に理解できます。

そんなに難しい話ではなく、力学的エネルギー保存の法則と運動量保存の法則がわかれば大丈夫です。

ということで、ここからは物理の話になります。

垂直跳びの高さとジャンプした瞬間の速さの関係式

垂直跳びの高さ：Ｈ

重力加速度：ｇ

体重：ｍ

ジャンプする瞬間の初速度：V

とします。

ジャンプした瞬間、足は地面から離れ、身体に加わる力は重力以外ありません。

体重も重力加速度も一定ですので、垂直跳びの高さというのはジャンプする瞬間の速度によってのみ決定されます。

エネルギー保存の法則より、

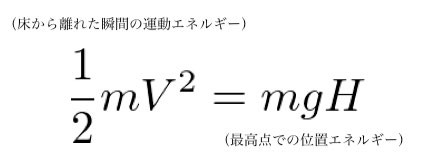
Vについて解くと

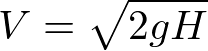
となり、ジャンプした瞬間の速度と垂直跳びの高さの関係が導かれます。

ジャンプした高さがわかればジャンプした瞬間の速度もわかることになります。

ジャンプした瞬間の速度とジャンプした瞬間に受ける力の関係

ジャンプした瞬間の速度は地面から受けた力（床反力）によって決定されます。

（床反力とは、自分が地面を押す力と反対方向に働く力のことです。これは作用反作用の法則で理解できます。高校物理では垂直抗力などと言ったりします。）

受けた床反力をFとし、受けた時間をｔとすれば、力積はFｔとなります。

床反力を貰う前の速度は0であり、地面から離れた瞬間床反力は0になるため、運動量保存の法則より、

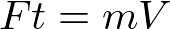
となります。

エネルギー保存の法則から導き出された

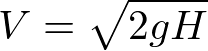
と

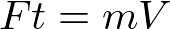
から、V（ジャンプした瞬間の速度）に代入してかつH（垂直跳びの高さ）について解くと

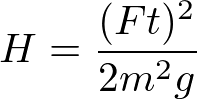
となって、垂直跳びと体重の関係式が出来上がります。

重力加速度は一定なので、垂直跳びの高さというのは床反力による力積の２乗に比例し、体重の２乗に反比例することがわかります。

仮に、体重が減ったとしても出せる力積が変わらないとすれば、体重以外は全て定数とみなせますので、体重以外をすべて定数とみなせば

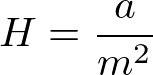
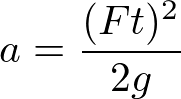
となり、書くことができ、わかりやすい式が完成します。

２乗に反比例するということは、痩せれば痩せるだけ加速度的にジャンプ力が上がっていくということです。

これらのことから、現時点でのジャンプ力がわかれば痩せた時のジャンプ力がわかることになります。（痩せたときの力積が変化しない場合）

これにより、垂直跳び100cm目指していたときに、いかほどの体重になればそのジャンプ力を得られるのかといったことがわかります。

では実際に計算してみましょう

自分のお話です。

この前に、3mの天井に向かってジャンプしたところ、天井に1cmの余裕をもって触ることができました。

靴を履いた時の自分の指高は238cmであるため、ジャンプ力は63cmとなります。

靴や服を着た時の体重は約93kgですので、このときの係数αを計算すると、

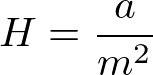
ですので、

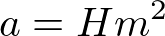
となり、

現時点で自分が出せる力であるαは、α ＝ 63cm × 93kg × 93kg ＝ 544887となります。

痩せたとしても、出せる力であるαが一定であると仮定の元に計算すると、以下のようになります。

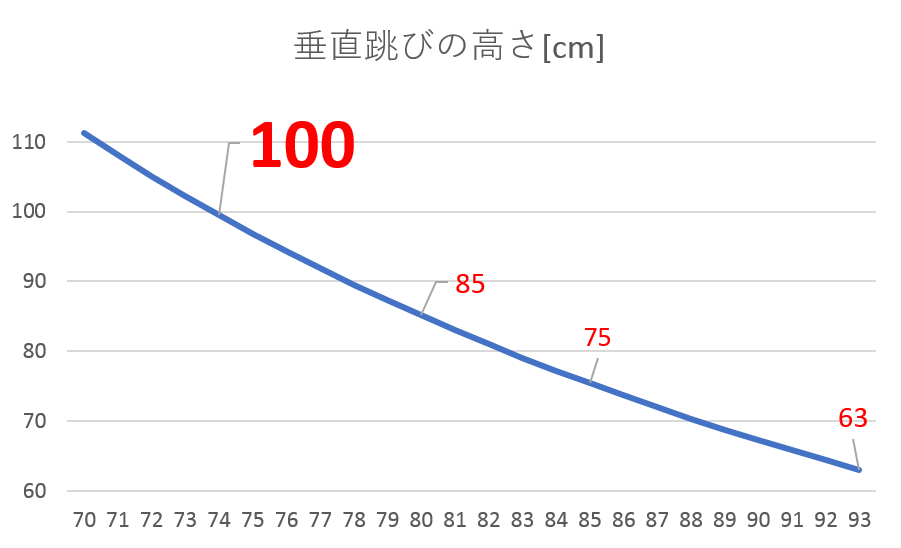
体重が減れば減るほど加速度的にジャンプ力が上がっています。

もし筋力が一定だとした場合、今のままだと74kgまで体重を落とせば垂直跳びが100cmとなります。

マイケルジョーダンは122cm跳べたとのことですが、自分の場合体重が67kgにならないとこんなに跳ぶことはできません。

しかも筋力を保ったままというありえない仮定のも元での結果です。

2017年のダイエットでは体重97kgから77kgまで体重を落としました。

あと３kg落として74kgになると、フィジークの大会に出られるぐらいの絞りになります。

2019年はスクワットでさらに筋肉もついたはずなので、絞ったときにこれ以上の体重になるはずです。

2019年の11月1日から減量を開始するつもりですが、78kgまで落としたときに100cm跳ぶためには現在どれ位跳ぶ必要があるか計算しました。

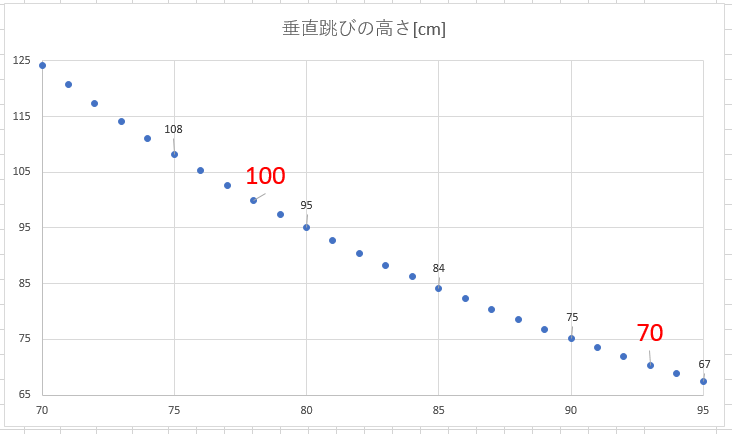
こうなりました。

つまり、現時点（体重93kg）で70cm跳ぶ必要があります。

しかもこれは筋力が一定と仮定した場合です。

15kgも痩せるとスクワットの重量もかなり下がってしまうでしょう。

実際に痩せた時に100cm跳ぶためには、現時点で70cm以上余裕を持って跳ぶことができる能力が必要です。

スクワットのMAXと垂直跳びの高さが相関すると仮定すると

本来の話は単純ではありませんが、また仮定のお話をします。

垂直跳びの高さは

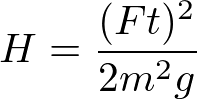
となることは説明しました。

このＦｔという値は力積のことで、地面から受ける床反力のことです。

床反力を得るためには地面を蹴る（キックする）必要があり、そのキック力が完全にスクワットと相関すると仮定します。

また、床を蹴る時間もそこまで変化しないと考えるので一定とします。（測定したことないので本当かどうかわかりません。ｔは0.3秒から0.5秒程度というお話。）

そう考えると、体重が変わらないとすれば、垂直跳びの高さはスクワットの重量の２乗に比例します。

ここで、自分の話になります。

現在の自分の身体能力（パラメータ）は、

体重93kg、垂直跳び63cm、ATGスクワットのマックスが175kgなので、代入すると

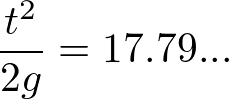
となります。

ｔを一定と考え、スクワットが垂直跳びの高さに完全に相関すると仮定すれば、スクワットの重量によってジャンプ力はこのようになります。

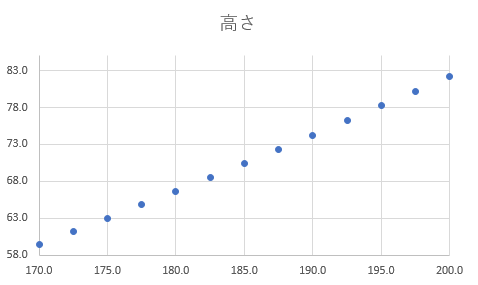
先の考えで、体重が93kgの場合、70cm跳ぶことができたら78kgになったときに100cm跳ぶことができるので、グラフよりスクワットの重量は、185kg必要なことがわかります。

やせればスクワットの重量はどうしたって下がる

最初に、体重が減っても筋力が変化しなければ、垂直跳び１００ｃｍ跳ぶため、現在の体重で７０ｃｍ跳ぶ必要があることを書きました。（現時点と比べるとジャンプ力が7cmほど足りない。）

次に、体重が一定のもとで、スクワットの重量と垂直跳びの高さが相関すると考えた中では、体重９３ｋｇで垂直跳び７０ｃｍ跳ぶためにはスクワット１８５ｋｇ上げる必要があると書きました。（現時点と比べるとスクワットのMAXが15kgほど足りない）

しかし、これらはどちらも現実的でなく、実際のところ体重が変化すれば筋力ないしスクワットの重量というのは変化します。

・体重が1kg減ると、スクワットの重量も1kg減る

・体重が78kgになったときに100cm跳べる

・体重が95kgで、スクワットが200kgできて、かつ80cm跳べる

と仮定したときのグラフは以下のようになります。

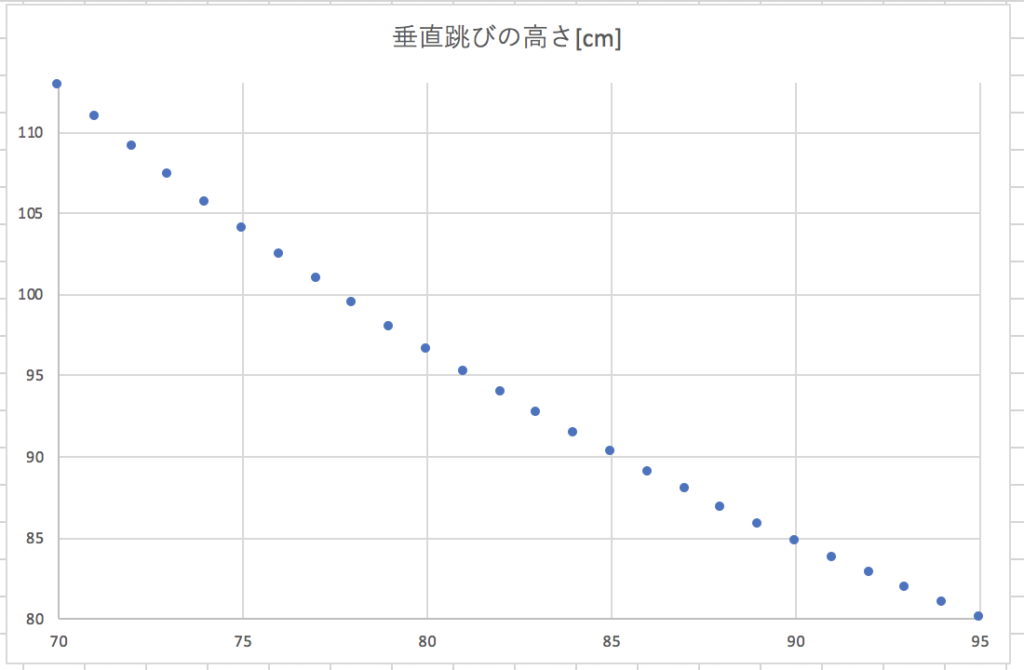
つまり、体重が78kgのときにスクワットが183kgできれば良いことになります。

これは自体重の2.34倍にあたります。

仮説と実験、そして立証

最後に現実的な話をしましたが、本当にこのようなグラフになるかわかりません。

そもそも体重が1kg減ったらスクワットが1kg減るかどうかもわかりません。

らもっと減るかもしれないし減らないかもしれない。

もっと減るようであれば、スクワット２００kgじゃ全然足りないし、減らないなら２００ｋｇで十分となります。

そもそも体重９５ｋｇでスクワットが２００ｋｇ、そして垂直跳びが８０ｃｍというのが達成できるか不明です。

・体重が９５ｋｇ、スクワットが２００ｋｇで垂直跳びが８０ｃｍ

・体重が１ｋｇ減るとスクワットのマックスが１ｋｇ減る

・ジャンプしたときの床反力はスクワットと相関する

・ジャンプしたときの床反力が得られる時間は体重とスクワットの重量が変わっても変化しない

といった根拠のもとで、体重が７８ｋｇになった時点で垂直跳びは約１００ｃｍとなるわけです。

これらの話はすべて仮説です。仮説を立証するためには実験しなければなりません。

しかし、この仮説を立証するのは困難を極めます。

測定するパラメータ自体はいたってシンプルで

・体重（体重計）

・ジャンプ力（デジタル垂直跳び測定器）

・スクワットのマックス（RM換算値でもよいだろう）

で実験できます。

（本格的にやるなら測定時間や気温、体温なども測定したほうがよい。）

しかし、これはあくまで個人での話であって他人と比較できません。

例えば

A：体重７０ｋｇ 垂直跳び９０ｃｍ スクワットMAX１８０ｋｇ

B：体重９０ｋｇ 垂直跳び８０ｃｍ スクワットMAX２００ｋｇ

の二人の数値を比べて表をつくっても何の意味もありません。

なぜならAとBは身長も違えば跳び方も違い、骨格も違いありとあらゆるものが違います。

この実験を立証するには、一人ひとりを２０ｋｇ程度痩せさせて、１ｋｇ痩せるたびにジャンプ力とスクワットマックスを測定しなければなりません。

これは相当時間かかるし、実験する人として１００人用意したとしてもそのうちいったい何人が２０ｋｇも痩せられるでしょうか。

こういった実験は不可能であり、論文を探していてもでてきません。

そもそもこんなことに興味を持っている人もいないかもしれません。

ここまで大規模な実験をやっても得られるお金はなにもないからスポンサーもつかないし研究費がそもそもありません。

どっかの大富豪が趣味で実験する以外方法がないのです。

実験します

仮説を立証することはできませんが実験はできます。

たったN＝１のサンプルですが、自分でやってみようと思います。

必要なものはデジタル垂直跳び測定器（お値段４万円）と体重計とスクワットができる環境です。（本格的にやるなら温度計と体温計も必要）

実験開始は２０１９年の１１月１日からになります。

そこから減量を初めて、１ｋｇ痩せるたびにスクワットのマックスと垂直跳びの高さを計測していきます。

2019/11/1の時点での体重が９５ｋｇで、スクワットマックスが２００ｋｇの予定です。

また、痩せたときの体重は７８ｋｇを目標とし、１７ｋｇの減量になります。

１７ｋｇ痩せることによってジャンプ力がどれほど変化していくのか、スクワットのマックスはどれほど減るのか楽しみにしていてください。

まとめ

・ジャンプ力は体重の２乗に反比例する

・体重が軽ければ軽いほど加速度的にジャンプ力が上がる

・小さい人はジャンプ力を上げやすい

・スクワット２００ｋｇできて体重が７８ｋｇになっても垂直跳び１００ｃｍいくかわからない

・体重が９５ｋｇで垂直跳びが８０ｃｍならほぼ間違いなく体重が７８ｋｇのときに垂直跳びは１００ｃｍに到達する。

・２０１９年１１月１日より『スクワットと体重と垂直跳びの関係』という実験を行う

感想

体重９５ｋｇ、スクワット２００ｋｇで垂直跳び８０ｃｍっていうのは正直無理です。

現在体重９３ｋｇ、スクワット１７５ｋｇで垂直跳びが６３ｃｍなのであまりにも現実的ではないです。

なので、おそらくスクワット２００ｋｇ上げることができて、体重が７８ｋｇになったとしても垂直跳び１００ｃｍにはなれないでしょう。

しかし、減量を開始と同時にクイックリフトのトレーニングを本格的にやり、かつプライオメトリクス（ジャンプトレーニング）も導入します。

さらに言えば、これはあくまで垂直跳びの話で、自分は助走をつければ垂直跳びと比べて＋２０ｃｍほど高く跳べます。

なぜこんなことができるかというと、水平方向のエネルギーを効率よく床反力に変えられるためです。

そういったことをすべて考慮すれば、やはりATGスクワットを２００ｋｇできてかつ体重が７８ｋｇ程度になればダンクできるんじゃないかなと思います。

もし７８ｋｇになってもダンクできなければ、さらに減量してもいいし、APL concept1買ってもいいし、赤道直下の国に行ってもいいし、なんならキリマンジャロに登ったっていいです。

最後に一言

フォースプレート（床反力計）欲しいなと思ったら、お値段なんと200万円！